摘要:本文是看《大话数据结构》栈章节的学习总结
正文:
栈的应用——四则运算表达式
栈的应用场景有很多,如浏览器的后退,编辑软件的回退等,今天要谈的是栈的基本应用之四则运算表达式(中缀转后缀表达式)
大家都知道用计算器可以很方便的计算出两数运算的结果,但是如果遇到有优先级的四则运算,计算器又是如何去精确的计算出结果呢?
在20世纪50年代有一个叫**Jan Łukasiewicz的波兰数学家想到了一种不需要括号的后缀表达式,我们称为逆波兰表示法** ,逆波兰记法不需要括号来标识操作符的优先级
中缀转后缀表达式
我们平时所用的标准四则运算表达式,如:
150-(7+5)*2+30*2
叫做中缀表达式,因为所有的运算符号都在两个数字之间,现在我们通过使用栈将其转为后缀表达式
规则:
从左到右遍历上面中缀表达式的每个数字符号
- 如果是数字则直接输出
- 如果是符号则判断与栈顶中的符号优先级,是右括号的或者比栈顶中符号优先级低的依次去括号出栈输出
- 否则在栈中等待最后遍历完依次输出
转换过程
- 按照上述规则依次遍历
150-(7+5)*2+30*2,150是数字直接输出,-号进栈,第三个是左括号也是符号依然进栈,7是数字直接输出,如下图一所示。
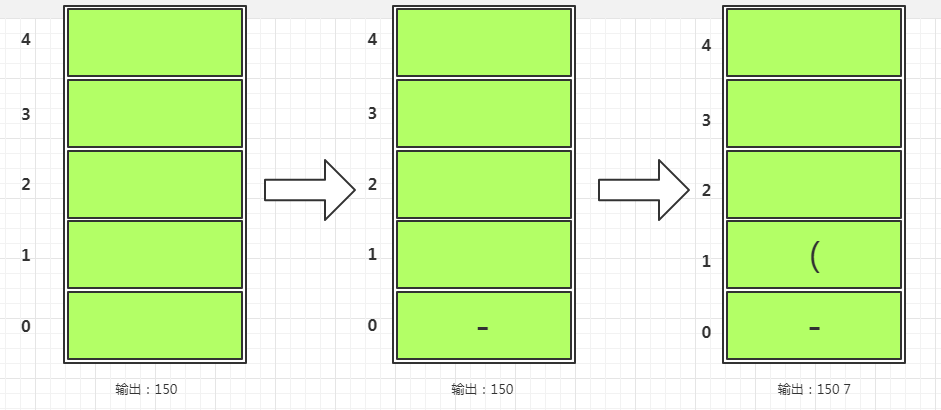
- 下面接着
+号进栈,5输出,接下注意的是右括号,遇到右括号需要匹配前面的左括号,并依次去括号出栈输出(输出了+)。接着*号进栈,2输出,如下图二所示。
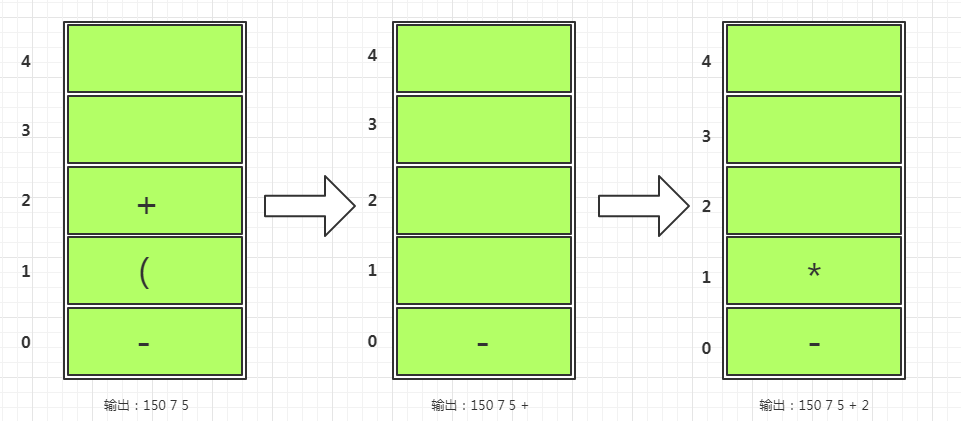
- 此时栈顶是
*,然后+号准备进栈,对比发现+优先级低于栈顶,则栈顶元素依次输出,完了后+号进栈 。接着30输出,*比栈顶+优先级高,直接进栈不输出,然后2输出。如下图三所示。
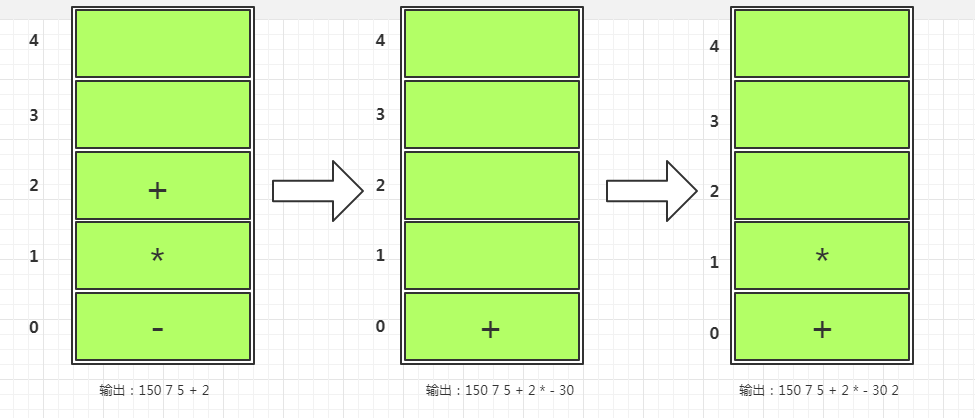
- 最后遍历结束栈中符号依次输出,最终的后缀表达式结果是**
150 7 5 + 2 * - 30 2 * +**
后缀表达式计算结果
上述结果:**150 7 5 + 2 * - 30 2 * +**, 可能很多人问转这个有什么用,接下来看的是该后缀表达式的计算过程。
计算规则:从左到右遍历每个数字和符号,遇到数字就进栈,遇到符号将处于栈顶的两个元素出栈并运算,运算结果进栈,一直到最后算出最终结果
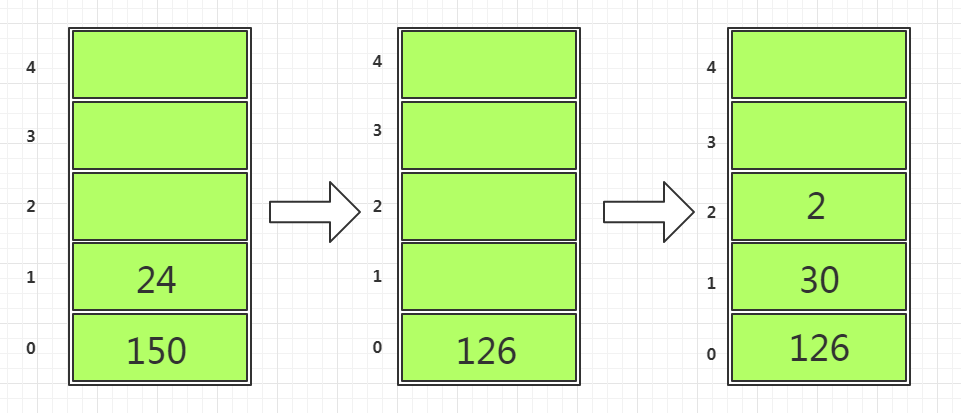
- 150 7 5依次进栈,
+号是符号,将栈顶的 7 5出栈并运算(+),结果是12并进栈,2是数字同样进栈。如下图四所示。
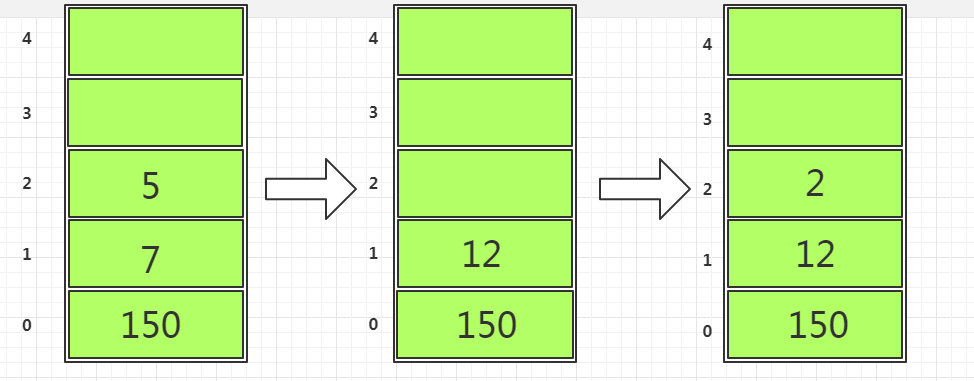
- 接着是
*号,将栈顶的两个元素运算并重新入栈(12 2);然后是-号,栈顶两个元素分别是*150 24,结果是126入栈;然后数字30 2**依次入栈。如下图五所示。
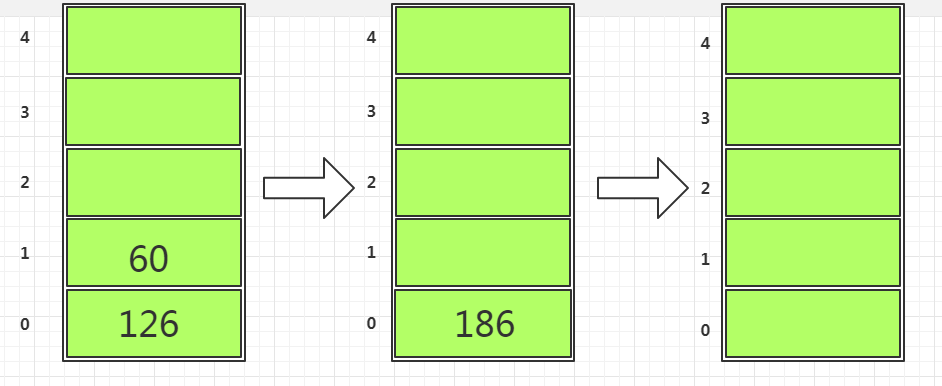
- 遍历到
*,将栈顶元素30 2运算并重新进栈,最后是+号,所以结果是186出栈,栈变为空。如下图六所示。
上述过程都充分的利用了栈的后进先出特性来处理的,所以该表达式的转换和计算是栈的经典应用之一,对理解栈本身也有很大的帮助~
